本帖最后由 首经贸 于 2022-12-2 15:41 编辑
学姐介绍:
一诺学姐,考研初试总分400+,702专业135+,916公共管理综合140+,初试复试排名前三,善于归纳总结抓住考试重点难点,为考生提供高效学习秘诀和应试技巧,指导同学们精准、高效有战略的复习。
导论
1、统计学
举例:市场研究,财务分析,经济预测
统计学是收集、处理、分析、解释数据并从数据中得出结论的科学。
2、描述统计与推断统计 (1)描述统计
第三章、第四章
描述统计研究的是数据收集、处理、汇总图表、描述概括与分析等统计方法。
(2)推断统计
第七章参数、估计、假设、检验
推断统计是研究如何利用样本数据来推断总体特征的统计方法,即抽出部分个体样本推断总体特征。
3、统计数据的类型
(1)分类数据
比如:性别男女
它是只能归于某一类别的非数字型数据,数据表现是类别,是用文字来表述的。
(2)顺序数据
比如:一等奖学金、二等奖学金、三等奖学金
它是某一有序类别的非数字型数据,顺序数据也是类别,但类别是有序的。
(3)数值型数据
它是按数字尺度测量的观察值,其结果表现为具体的数值。
分类数据和顺序数据说明的是事物的品质特征,通常用文字表述,其结果均表现为类别,因此也称为定性数据或品质数据;数值型数据说明的是现象的数量特征,通常是用数值来表现的,因此也称为定量数据或数量数据。
(4)按搜集方法不同,分为观测数据和实验数据
①观测数据
调查、观测得到的,没有人为控制条件。
②实验数据
实验组、控制组
(5)按时间不同,分为截面数据和时间序列数据
①截面数据
近似时间点:今天不同行业GDP
②时间序列数据
不同时间段:不同年份的GDP
4、统计学中几个基本概念:
(1)总体:它是包含所研究的全部个体(数据)的集合,组成总体的每一个元素称为个体。按照总体所包含元素数目可分为有限总体和无限总体。
(2)个体:组成总体的每个元素。
(3)样本和样本量:样本是指从总体中抽取一部分元素的集合,样本也是总体的一个子集;样本量是构成样本元素的数目。
(4)参数:它是描述总体特征的概括性数字度量,是研究者想要了解总体某种特征的数量表现。
(5)统计量:它是描述样本特征的概括性数字度量,是根据样本数据计算出来的一个量,是为了实现推断统计,对原始数据进行运算,利用有用的样本信息构造的不含任何未知参数的样本函数。统计量是随机变量,是统计推断的基础。
比如:总体有500个,总体数量太多,不可能一一调查,随机选择30个,求出平均数,进行估计计算。
(6)变量:它是描述现象某种特征的概念,特点是从一次观测值到下一次观测值呈现出的变化的差别。
①分类变量:描述事物的一个类别的一个名称,取值是分类的一个数据。
②顺序变量:事物有序类别的一个特征取值是顺序数据。
数据的搜集
1、数据的来源?
数据的来源有两个:直接来源和间接来源
①间接来源的数据称为二手数据,它是指研究对象的原信息已经存在,对数据进行重新整理、加工可以直接用于分析的数据。
优点:
获取方便,采集成本低,能够很快得到并利用。
缺点:
针对性差、无法保证数据的准确性和及时性。
在使用二手数据之前要进行评估,即二手数据是谁搜集的、什么时候搜集的、为什么而收集的、用什么办法收集的;还要注意数据的定义、计算口径和方法,避免错用、滥用、误用;还要注明数据来源,尊重他人劳动成果。
②直接来源的数据是经过自己的调查或实验等直接实践活动取得的一手数据。
2、概率抽样:
概率抽样也称为随机抽样,是指遵循随机原则进行的抽样。
特点:
①抽样采取随机原则,每个单位都有一定的概率被抽中。
②每个单位被抽样中的概率是已知的或者是可以计算的。
③在用样本估计总体目标量的时候要考虑每个单位被抽中的概率,估计量不仅与样本单位的观察值有关,而且与入样概率有关,能够用来估计总体参数。
3、常见的概率抽样方式?
每一种抽样优缺点找课本补充背诵。
(1)简单随机抽样:是从总体N个单位中随机抽取n个单位作为样本,每个单位以相等的概率入选,是最基本的抽样方法,其他抽样方法的基础。
优点:简单直观,抽样框比较完整,可以直接从总体中抽取样本。
缺点:如果抽取的总体比较大,则构造相应的抽样框是不容易的。抽取的单位比较分散,也会加大调查的难度。没有其他的一个辅助信息,提高效率。
(2)分层抽样:是将总体单位按照不同的特征或规则划分不同的层,然后从每层中独立、随机地抽取一定数量的单位组成样本。
优点:样本的结构和总体结构是比较相近的。为组织实施调查提供了方便。对总体参数进行估计时,可以用各层的目标量进行估计。
(3)整群抽样:是先将总体中部分单位合并为组,即称为群,然后以群为单位直接抽取样本,在对入选群中的所有单位实施调查。
优点:抽样只需按照群,构造抽样框,简化了工作量。调查地点相对比较集中,节省了相应的调查费用。
缺点:估计误差比较大。
(4)系统抽样:是先将总体各单位按照一定的顺序进行排序,在一定范围内随机抽取一个单位定为初始单位,再按照一定规则选取其他单位组成样本。
优点:操作比较简便,有效的提高估计精度。
缺点:对方差的估计比较困难的。
(5)多阶段抽样:先抽取群,但不是直接调查群内所有的单位,而是在每个群中抽取样本单位。因接受调查的单位需经两个步骤产生而命名二阶段抽样,将该方法延续,使抽样的段数增多,就成为多阶段抽样。
优点:保证样本相对集中,节约了调查费用。不包含基阶段的抽样框,可以在更广的范围内展开。
4、常见的非概率抽样方式:
不是根据随机的原则,只是根据对数据的一个需求,进行的一种方式。
优点:就成本比较低,容易实施。
缺点:没有办法对总体进行估计。
(1)方便抽样:调查过程中由调查员依据方便的原则,自行确定入抽样本的单位。
(2)判断抽样:指研究人员根据经验、判断和对研究对象的了解,有目的地选择一些单位作为样本。
(3)自愿抽样:指被调查者自愿参加,成为样本中的一分子,向调查人员提供有关信息。
缺点:结果是有偏的。
(4)滚雪球抽样:往往使用于对稀少群体的调査中。在滚雪球抽样中,首先选择一组调査单位,对其实施调査之后,再请他们提供另外一些属于研究总体的调查对象,调查人员根据所提供的线索,进行此后的调查。
(5)配额抽样:类似于概率抽样中的分层抽样,它是首先将总体中的所有单位按一定的标志(变量)分为若干类,然后在每个类中采用方便抽样或判断抽样的方式选取样本单位。
5、概率抽样和非概率抽样的区别?
(1)非概率抽样适合探索性的研究和市场调査中的概念测试,其特点是操作简便、时效快、成本低,而且对于抽样中的统计学专业技术要求不是很高。
如果调查的目的是用样本的调查结果对总体相应的参数进行估计,并计算估计的误差,得到总体参数的置信区间,就应当使用概率抽样的方法。
(2)概率抽样是依据随机原则抽选样本,此时样本统计量的理论分布是存在的。概率抽样的技术含量更高,无论抽选样本和对调查数据进行分析,都要求有较高的统计学专业知识,调查的成本也比非概率抽样的调査成本高。有时在一项研究性项目中,可以把概率抽样和非概率抽样相结合,发挥各自的特点,满足研究中的不同需求。
6、搜集数据的基本方法?
区分搜集数据和调查方法。
(1)自填式问卷调查:在无调查员协助的情况下由被调查者自己完成调查问卷。
(2)面访式问卷调查:调查员与被调查者面对面提问、被调查者回答。
(3)电话式调查问卷:通过各种电讯工具向被调查者实施调查。
(4)观察式调查:调查员通过直接观察的方式获取信息。
调查方式:普查、统计报表、抽样调查、重点调查、典型调查、代表抽样。
7、数据的误差
数据的误差泛指通过调查得到的数据与研究对象真实结果之间的差异,数据的误差有抽样误差和非抽样误差两种。
(1)抽样误差:由于抽样的随机性引起的样本结果与总体真值之间的误差。它描述的是所有样本可能的结果与总体真值 之间的平均性差异。并且是一种随机性误差,只存在于概率抽样中。
抽样误差的影响因素:
①样本单位数目,数目越大,误差越小 ②总体差异程度,差异越大,误差越大 ③抽样方法:采取不重复抽样 ④抽样组织形式,不同组织形式抽样误差大小不同
(2)非抽样误差:指除抽样误差之外的,由于其他原因引起的样本观察结果与总体真值之间的差异。无论是概率抽样、非概率抽样,或是在全面性调查中,都有可能产生非抽样误差。
8、误差的几种表现及产生原因?
(1)抽样框误差:统计推论的错误是由于抽样框的不完善造成的,把这种误差称为抽样框误差。
(2)回答误差:指被调查者在接受调查时给出的回答与真实情况不符。
而导致回答误差的原因有多种,主要有:
①理解误差; ②记忆误差; ③有意识误差。
(3)无回答误差:被调査者拒绝接受调査,调查人员得到的是一份空白的答卷。
无回答误差有时是随机的,有时是系统性的。
解决无回答的系统性误差的途径主要有:
①预防,即在调查进行前做好各方面的准备工作,尽量把无回答降到最低程度;
②当无回答出现后,分析无回答产生的原因,采取一些补救措施。
(4)调査员误差:由于调查员的原因产生的误差。
(5)测量误差:由于测量工具不同产生的误差。
数据的整理与展示
1.数据的预处理?
它是在对数据分类或分组之前所做的必要处理,包括数据的审核、筛选、排序等。
(1)数据审核是检查数据中是否有错误,对于通过调查取得的原始数据主要从完整性和准确性两个方面去审核,而对于通过其他渠道获得的二手数据应着重审核数据的适用性和时效性。
(2)数据筛选是根据需要找出符合特定条件的某类数据。
(3)数据排序是按一定顺序将数据排列,以便研究者通过浏览数据发现一些明显的特征或趋势,找到解决问题的线索。
2.分类数据的整理和图示?
(1)整理
①频数:是落在某一特定类别或组中的数据个数。
②频数分布表:将各个类别及落在其中的相应频数全部列出,并用表格的形式表现出来。
③比例:是一个样本(或总体)中各个部分的数据与全部数据之比,通常用于反映样本(或总体)的构成或结构。
④百分比:将比例乘以100得到的数值。
⑤比率:是样本(或总体)中不同类别数据之间的比值。
(2)分类数据的图示
①条形图 ②帕累托图 ③饼图 ④环形图
3.顺序数据的整理?
向上累积:10%+20%=30% 向下累积:100%-30%=70%
①累积频数:将各有序类别或组的频数逐级累加起来得到的频数,有向上累积和向下累积。
②累积频率:将各有序类别或组的百分比逐级累积起来,也有向上累积和向下累积。
4.数值型数据的分组?
分组有单变量值分组(适用于数据较少的离散型变量)和组距分组(适用于数据多的连续型变量)。
(1)分组步骤:
①确定组数:一般来说组数k区间为5≤k≤15,确定组数的公式为k=1+lgn≒lg2。
②确定组距:组距是一组上限和下限的差,计算方法是数据最大值减去最小值除以组数(要采用5或10的倍数)。
③根据分组整理成频数分布表。
(2)组距分组的注意事项
①组距分组需要遵循“不重不漏"的原则即:
“不重”是指一项数据只能分在其中的某一组,不能在其他组中重复出现;“不漏"是指组别能够穷尽,即在所分的全部组别中每项数据都能分在其中的某一组,不能遗漏。
为解决“不重”的问题,统计分组时习惯上规定“上组限不在内”,即当相邻两组的上下限重叠时,恰好等于某一组上限的变量值不算在本组内,而计算在下一组内。
比如:一组:70—80;二组:80—90
80属于二组
5.数值型数据的图示?
①直方图(分组数据)
②茎叶图(未分组数据)side width=10,则数据组11、12、13
③箱线图(未分组数据)重点复习一下
6.直方图与条形图的联系与区别?
联系:都是用矩形来表示数据的分布情况,当矩形宽度相等时都是用高度来表示数据分布情况。
区别:
①直方图的高度宽度均有意义,高度表示每一组的频数或频率,宽度表示各组组距,面积表示各组频数的多少;条形图的宽度是固定的,高度表示频数多少。
②直方图的各矩形是连续排列的,而条形图是分开排列的。
③直方图是用来展示数值型数据,条形图用来展示分类型数据。
7.鉴别图形优劣的准则?
①能够在短时间内给读者提供大量的信息 ②能够反应数据的真实情况 ③应该是多维的 ④能够洞察问题的实质 ⑤能够将复杂的问题简明、明确、高效阐述出来
数据的概括性度量
1.集中趋势的度量?
集中趋势是指一组数据向某一中心值靠拢的程度,它反映了一组数据中心点的位置所在。
集中趋势的度量有众数、中位数、分位数、平均数,通常不同类型的数据采用不同的集中趋势测度值,低层次数据的测度值适用于高层次的测量数据,而高层次数据的测度值不适用于低层次的测量数据。
2.众数、中位数、平均数的关系和应用场合?
(1)关系:从分布的角度看,众数始终是一组数据分布的最高峰值,中位数是处于一组数据中间位置上的值,平均数是全部数据的算术平均。
①若数据分布为对称分布 ②若数据分布为左偏分布 ③若数据分布为右偏分布
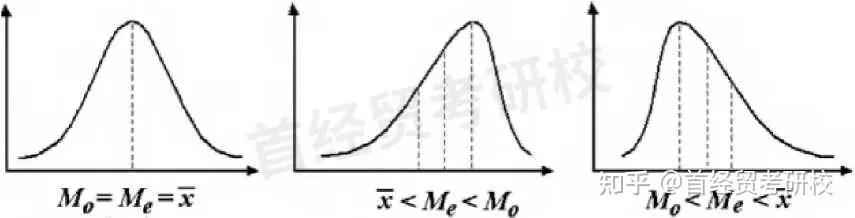
(2)众数、中位数和平均数的特点与应用场合
①众数是一组数据分布的峰值,不受极端值的影响。其缺点是具有不唯一性,众数只有在数据量较多时才有意义,当数据量较少时,不宜使用众数。众数主要适合作为分类数据的集中趋势测度值。众数不唯一。
②中位数是一组数据中间位置上的代表值,不受数据极端值的影响。中位数主要适合作为顺序数据的集中趋势测度值。
③平均数是对数值型数据计算的,而且利用了全部数据信息,它是实际中应用最广泛的集中趋势测度值。
当数据呈对称分布或接近对称分布时,3个代表值相等或接近相等,这时则应选择平均数作为集中趋势的代值。但平均数的主要缺点是易受数据极端值的影响,对于偏态分布的数据,平均数的代表性较差。因此,当数据为偏态分布,特别是当偏斜程度较大时,可以考虑选择众数或中位数。
3.离散程度的度量?
数据的离散程度,它反映的是各变量值远离其中心值的程度。数据的离散程度越大,集中趋势的测度值对该组数据的代表性就越差;反之,离散程度越小则代表性就越好。
离散程度的度量有异众比率、四分位差、极差、平均差、标准差、方差、离散系数。
(1)异众比率是指非众数组的频数占总频数的比例,用表示
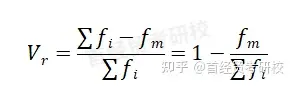
异众比率主要用于衡量众数对一组数据的代表程度。异众比率越大,说明非众数组的频数占总频数的比重越大,众数的代表性越差;反之,代表性越好。异众比率主要适合测度分类数据的离散程度,对于顺序数据以及数值型数据也可以计算异众比率。
(2)四分位差是上四分位数与下四分位数之差,用Qd=Qu-Ql表示。(先排序再计算)
四分位差反映了中间50%数据的离散程度,其数值越小,说明中间的数据越集中;其数值越大,说明中间的数据越分散。四分位差不受极端值的影响。
极差:一组数据的最大值与最小值之差称为极差,也称全距,用R表示。
其计算公式为:
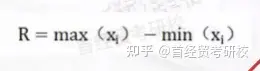
平均差:也称平均绝对离差,它是各变量值与其平均数离差绝对值的平均数。
方差:各变量值与其平均数离差平方的平均数。
标准差:方差的平方根。
4.相对位置度量的经验法则?
(全面背诵)
当数据对称分布时,经验法则表明:约有68%的数据在平均数 +1个标准差范围内;约有95%的数据在平均数 +2个标准差范围内;约有99%的数据在平均数 +3个标准差范围内。
当不是对称分布,则运用切比雪夫不等式(至少有
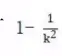
的数据落在 k 个标准差之内),则至少有75%的数据在平均数2个标准差范围内;至少有89%的数据在平均数3的标准差范围内;至少有94%的数据在平均数4个标准差范围内。
+1个标准差范围内:29 30 31 +3个标准差范围内:27 30 33
5.相对离散程度:
离散系数是一组数据的标准差与其相应的平均数之比。
计算公式为:
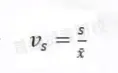
离散系数是测度数据离散程度的相对统计量,主要是用于比较不同样本数据的离散程度。离散系数大,说明数据的离散程度也大;离散系数小,说明数据的离散程度也小。
6.偏态与峰态的度量
(考前两个周背诵公式)
偏态及其测度:它是对数据分布对称性的测度。测度偏态的统计量是偏态系数,记作SK。
(1)未分组数据:
如果一组数据的分布是对称的,则偏态系数等于0;如果偏态系数明显不等于0,表明分布是非对称的。若 偏态系数大于1或小于一1,被称为高度偏态分布;若偏态系数在0.5〜1或-1~0.5之间,被认为是中等偏态分布;偏态系数越接近0,偏斜程度就越低。

抽样与抽样分布
(统计量概念找课本)
1.次序统计量:
设X1 X2 X3...Xn为总体X中抽取的样本, 称为第i个次序统计量,它是样本X1 X2 X3...Xn满足以下条件的函数:每当样本得到一组观测值X1 X2 X3...Xn时,将其从小到大排序,第i个值 就作为次序统计量 的观测值,而X1 X2 X3...Xn称为次序统计量。
2.充分统计量:
统计量加工过程中一点信息都不损失的统计量。
3.抽样分布:
抽样分布是从容量为N的总体中抽取容量为n的样本时,所有可能的样本统计值所形成的分布。假设从容量为N的有限总体中最多可以抽取m个容量为n的不同样本,那么把所有m个样本统计值形成频率分布,就是抽样分布。抽样分布是研究样本分布与总体分布之间关系的桥梁。
4.中心极限定理:设从均值为μ,方差为σ^2(有限)的任意一个总体中抽取样本量为n的样本,当n充分大时,样本均值X的抽样分布近似于服从均值为μ、方差为σ^2/n的正态分布。基于此,中心极限定理就是,随着样本量n的增大(n≥30),不论原来的总体是否服从正态分布,样本均值的抽样分布都将趋于正态分布,其分布的数学期望为总体均值μ,方差为总体方差的1/n。
(公式要进行背诵)
参数估计
(公式背诵并理解)
1.参数估计的基本原理?
参数估计就是用样本统计量去估计总体参数,在参数估计中,用来估计总体参数的统计量称为估计量,根据一个具体的样本计算出来的估计量的数值称为估计值。参数估计的方法有点估计和区间估计两种。
2.点估计和区间估计
(1)点估计:是用样本统计量的某个取值直接作为总体参数的估计值。
(2)区间估计:是在点估计的基础上,给出总体参数估计的一个区间范围,该区间通常由样本统计量加减估计误差得到。
3.置信区间和置信水平
(1)置信区间:由样本统计量所构造的总体参数的估计区间,其中区间的最小值称为置信下限,最大值称为置信上限。
(2)置信水平(置信度/置信系数):置信区间中包含总体参数真值的次数所占的比例。
4.评价估计量的标准?
评价估计量的标准有三个:无偏性、有效性、一致性。
①无偏性,指估计量抽样分布的数学期望等于被估计的总体参数。
②有效性,指对同一总体参数的两个无偏估计量(有效估计量一定是无偏估计量),有更小标准差的估计量更有效。
③一致性,指随着样本量的增大,点估计量的值越来越接近被估计总体的参数,即一个大样本给出的估计量要比一个小样本给出的估计量更接近总体的参数。
5.对置信区间的理解需要注意的地方?
(1)如果用某种方法构造的所有区间中有95%的区间包括总体参数的真值,5%的区间不包括总体参数的真值,那么用该方法构造的区间称为置信水平为95%的置信区间。(其他置信水平的区间也可这样表示)
(2)总体参数的真值是固定的、未知的,而用样本构造的区间则是不固定的。置信区间是一个随机区间,若抽取不同的样本,用该方法可以得到不同的区间。
(3)在实际问题中,进行估计时往往只抽取一个样本,此时所构造的是与该样本相联系的一定置信水平(例如95%)下的置信区间。由于用该样本构造的区间是一个特定的区间,而不再是随机区间,所以无法知道这个样本所产生的区间是否包含总体参数的真值。我们只能希望这个区间是大量包含总体参数真值的区间中的一个,但它也可能是少数几个不包含参数真值的区间中的一个。
假设检验
(计算题考的概率比较大)
1.假设检验和参数估计的区别
参数估计和假设检验是统计推断的两个组成部分,它们都是利用样本对总体进行某种推断,但推断的角度不同。参数估计讨论的是用样本统计量估计总体参数的方法,总体参数在估计前是未知的。而在假设检验中,则是先对的值提出一个假设,然后利用样本信息去检验这个假设是否成立。
2.假设检验的基本原理?
回答相关问题都要回答这一部分。
假设检验是指利用样本信息判断假设是否成立的过程,它是先对总体参数提出某种假设,然后利用样本信息判断假设是否成立的过程。
(1)原假设是研究者想收集证据予以反对的假设。
(2)备择假设通常是研究者想要收集证据予以支持的假设。
(3)假设检验的目的主要是收集证据拒绝原假设。
3.两类错误:
当原假设为真时拒绝了假设称为第一类错误,也称弃真错误,概率用α表示;当原假设为假时没有拒绝原假设称为第二类错误,也称取伪错误,概率用β表示。
4.P值的含义与决策步骤?
P值就是当原假设为真时所得到的样本观察结果或更极端结构出现的概率。用P值进行决策的准则是 值<α,拒绝H0;P值 >α,不拒绝H。 值<α,拒绝H0;P值 >α,不拒绝H。
如果P值很小,说明这种情况发生的概率很小,而如果出现了,依据小概率原理,就有理由拒绝原假设。P值越小,拒绝H0的理由越充分。
5.假设检验的基本步骤?假设检验的基本原理+P值+假设检验的基本步骤?
(1)根据问题的要求给出原假设H0,同时给出备择假设H1。
(2)在H0成立的前提下,选择合适的检验统计量,这个统计量应包括要检验的参数,同时它的分布已知。
(3)根据显著性水平α,按照备择假设H1和检验统计量的分布,写出小概率事件及其概率表达式。
(4)由样本值计算出检验统计量的数值,并查出对应的临界值。
(5)依据计算结果作出拒绝H0或接受H0的决策。
| 